Work Energy & Power

Work is done when a force moves its point of application along the direction of its line of action.

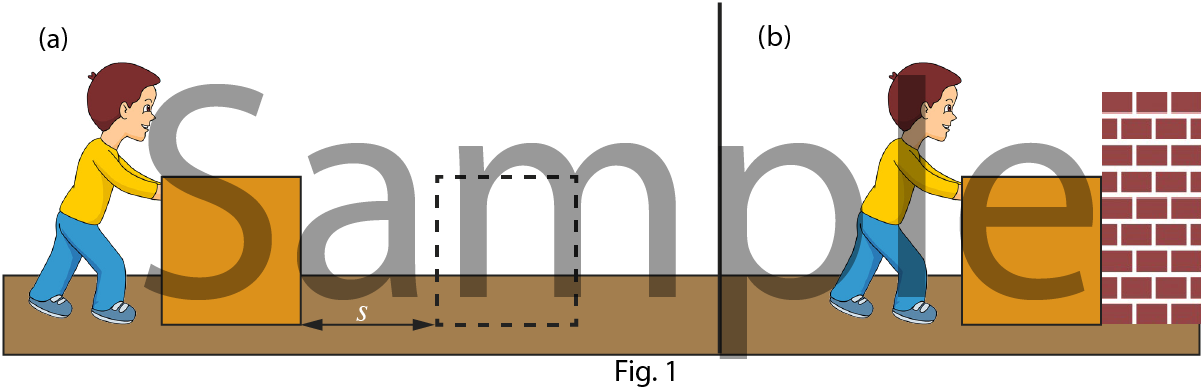
Consider case (a) in which a man pushing a block along the surface to move the block by distance s, whereas in another case (b) the person pushing the same block along the surface but against the wall and there is no displacement of the block.

In which case the work done is more?

In case (a) the work done is more because in physics a moving body is said to have more energy than an identical body at rest.

Work done cam be calculated by following three ways.

Work done by area under force displacement curve
Work done by a constant force
Work done by a variable force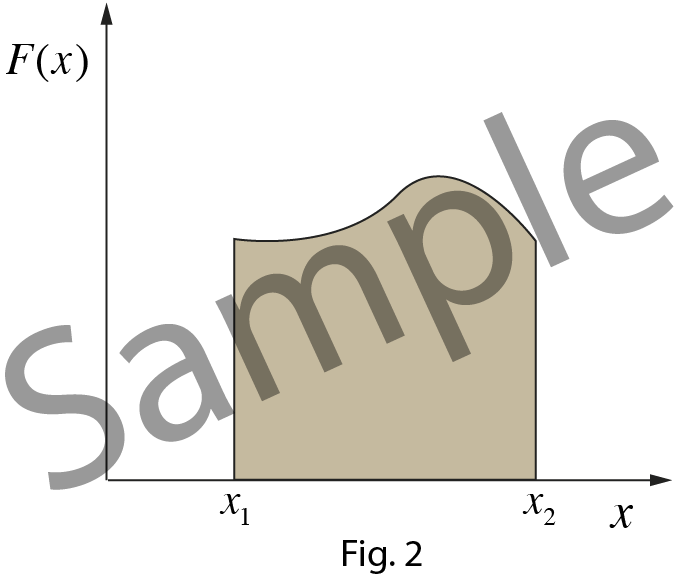

Work done by area under force displacement curve

Mathematically work done is,

$$ W = \int\limits_{{x_1}}^{{x_2}} {\overrightarrow F (x).d\overrightarrow x } $$

The above equation calculates the area under force – displacement curve.

Note: Area under force-displacement curve must be added with proper sign to obtain work done by the force.

Question 1. Find the work done by a constant force $ F $ in displacing an object by $ 3m $ as shown in the figure.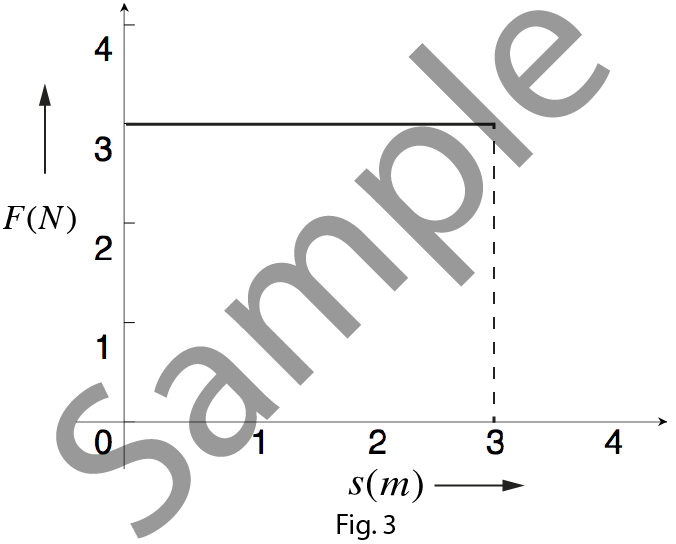

Solution: From the figure, constant force $F=3N$

Displacement $x$ of the object $=3m$

Work done is the area under the curve,

$$W=3\times3$$ $$W=9J$$

Question 2. A force $F$ acting on a particle varies with displacement $s$ as shown in the figure. Find the work done by the force in displacing body from $-2m$ to $2m$.

Solution: Work done by the force is equal to the area under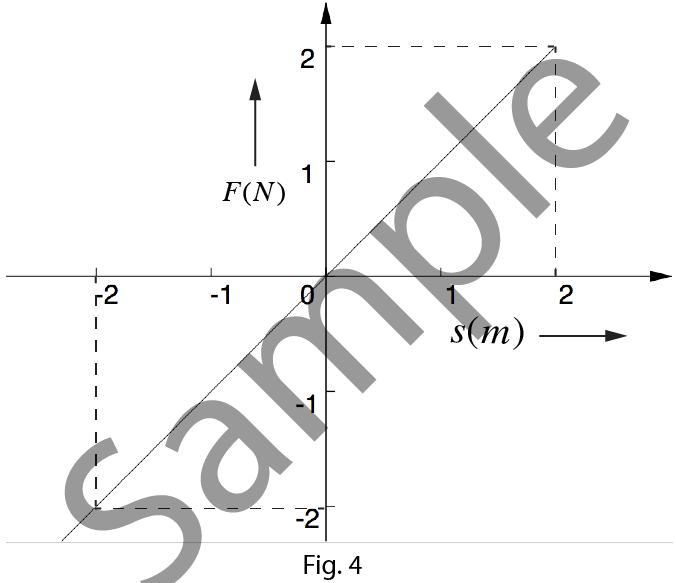 the curve.

$$Area = \frac{1}{2} \times ( - 2) \times ( - 2) + \frac{1}{2} \times 2 \times 2$$

Total area under the curve from position $-2m$ to $2m=4$ sq units.

$Work done=4J$

Work done by a constant force

Let us consider a man pulling a block of mass $m$ with a constant force $F$. Due to this force the body undergoes a displacement along the horizontal direction as shown in the figure.

As only the horizontal component (i.e. $F = \cos \theta $) of the force is responsible for displacement along horizontal direction.

Work done,$$W = (F\cos \theta ) \times s$$ or $$W = Fs\cos \theta $$ $$W = \overrightarrow F .\overrightarrow s $$

Therefore, work done is defined as the dot product of force and the displacement in the block due the action of that force.

Properties of work done

Work done is a scalar quantity as it is a dot product of two vector quantities $\overrightarrow F$ and $\overrightarrow s$.
Work done can be positive, negative or zero. It depends on the angle $\theta$ between the force $(F)$ and the displacement $(s)$.

When $\theta > 90^\circ $: work done $(W)$ is positive
When $\theta = 90^\circ $ work done $(W)$ is zero
When $\theta < 90^\circ $: work done $(W)$ is negative

Work done depends on the frame of reference

A. Inertial frame of reference

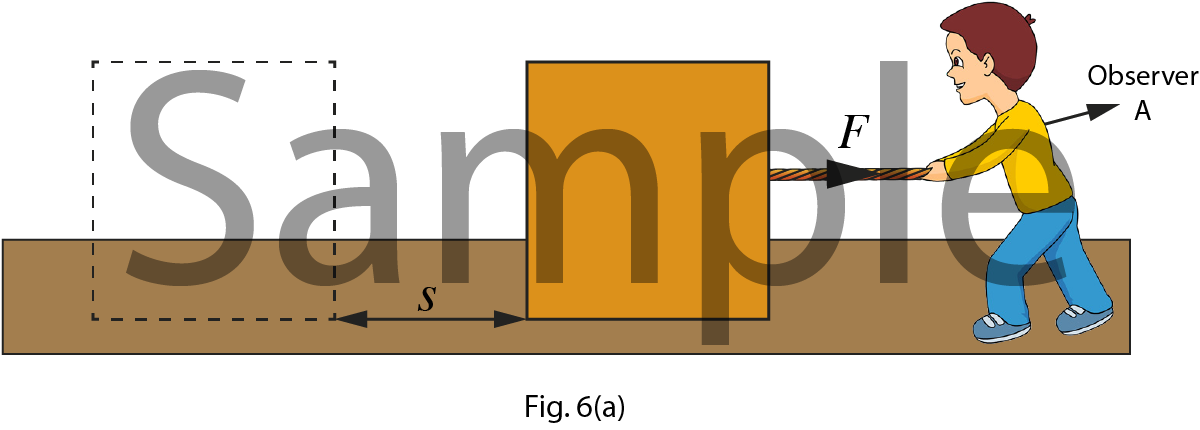
According to the observer A, the block has displacement $s$. Therefore the work done by the force is, $$W = \overrightarrow F .\overrightarrow s $$
In this case the train is running with constant velocity and $d$ & $s$ is the distance travelled by the train and block respectively. According to the observer A, the block has displacement $s$. Therefore the work done by the force is, $$W = \overrightarrow F .\overrightarrow s $$
According to the observer B, the block has displacement $(s+d)$. Therefore the work done by the force is, $$W = \overrightarrow F .\left( {\overrightarrow s + \overrightarrow d } \right)$$

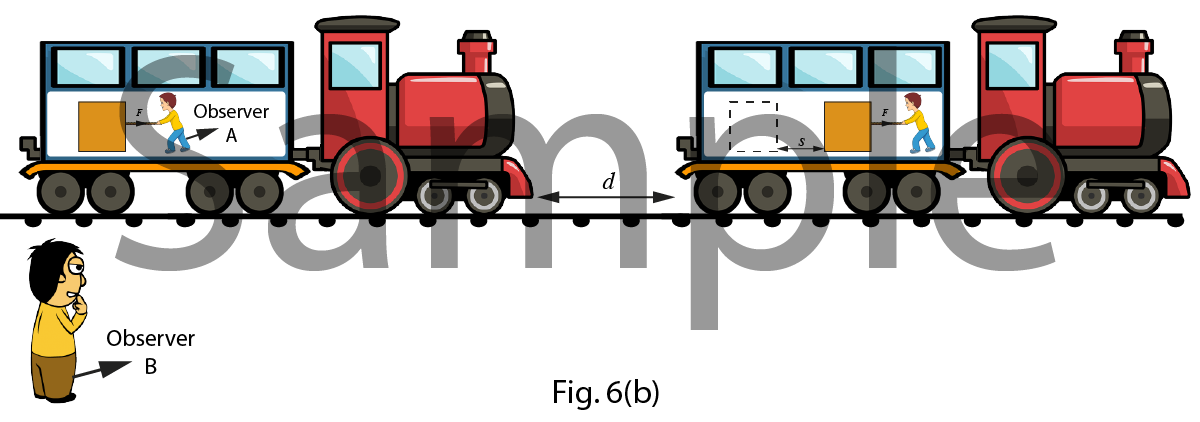
B. Non-inertial frame of reference

In this case the train is running with constant acceleration $a$ and $d$ & $s$ is the distance travelled by the train and block respectively. According to the observer A, the block has displacement $s$. Therefore the work done by the force is,$$W = \overrightarrow F .\overrightarrow s $$
According to the observer B, the block has displacement $(s+d)$ and the net force acting on the block in the horizontal direction is $(F-ma)$. Therefore the work done by the force is, $$W = \left( {\overrightarrow F - m\overrightarrow a } \right).\left( {\overrightarrow s + \overrightarrow d } \right)$$
According to the observer B, the block has displacement $(s+d)$. Therefore the work done by the force is, $$W = \overrightarrow F .(\overrightarrow s + \overrightarrow d )$$

Question 3. A body is displaced from $P$ $\left( {4\widehat i + 2\widehat j + 3\widehat k} \right)$ to $Q$ $\left( { - 3\widehat i - 2\widehat j + 5\widehat k} \right)$. Find the work done by a constant force $\overrightarrow F$ $\left( { 5\widehat i + 3\widehat j + 8\widehat k} \right)$.

Solution: Displacement of a body under the constant force $\overrightarrow F$ is ${\overrightarrow s _{PQ}}$.

$$\eqalign{
& {\overrightarrow s _{PQ}} = {\overrightarrow s _P} - {\overrightarrow s _Q} \cr
& {\overrightarrow s _{PQ}} = \left( {4\widehat i + 2\widehat j + 3\widehat k} \right) - \left( { - 3\widehat i - 2\widehat j + 5\widehat k} \right) \cr
& {\overrightarrow s _{PQ}} = \left( {7\widehat i + 4\widehat j - 2\widehat k} \right) \cr} $$
We know, work done $(W)$ is given by, $$\eqalign{
& W = \overrightarrow F .\overrightarrow s \cr
& W = \left( {5\widehat i + 3\widehat j + 8\widehat k} \right).\left( {7\widehat i + 4\widehat j - 2\widehat k} \right) \cr
& W = (35 + 12 - 16) \cr
& W = 31J \cr} $$

Question 4. A truck is moving with constant velocity $v=10 m/s$. A constant force $F=2 N$ relative to the truck is applied on a block of mass $m=1 kg$ which is initially at rest as shown in the figure. Find the work done on the block after 3 seconds as seen by,

Observer 1
Observer 2

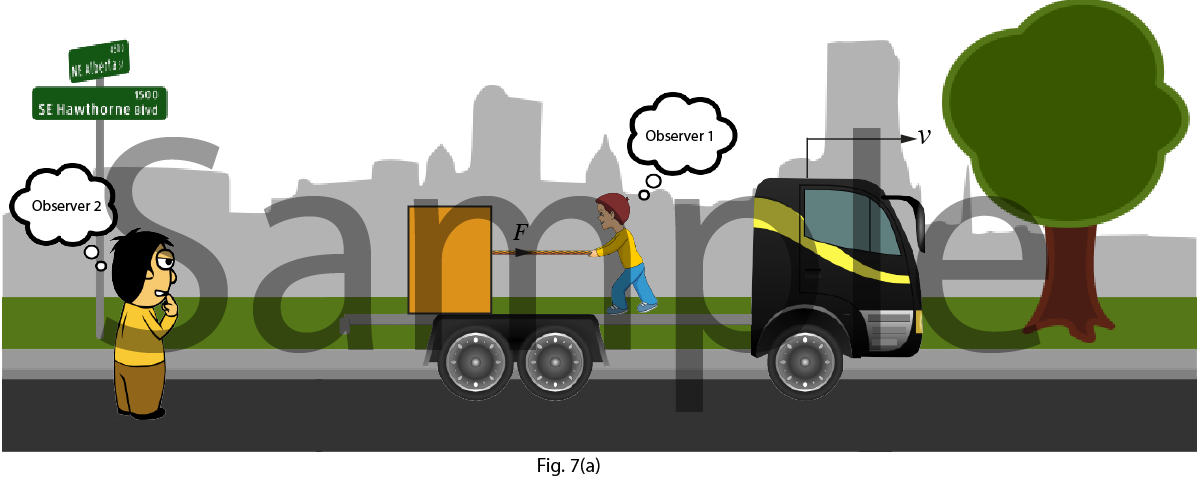
Solution: Displacement of truck $(s_1)$ in 3 seconds $=10\times 3=30m$

Acceleration of block due to constant horizontal force $F$ is $a=20m/s^2$

Displacement of block relative to truck $(s_2)$ in 3 seconds $=\frac{1}{2}at^2=\frac{1}{2}\times 2\times 9=9m$

Displacement of block as observed by observer 1, $=9m$

Work done $(W_1)$ is given by, $$\eqalign{
& {W_1} = \overrightarrow F .\overrightarrow s \cr
& {W_1} = 2 \times 9 \cr
& {W_1} = 18J \cr} $$

Displacement of block as observed by observer 2, $=(30+9)m$

Work done $(W_2)$ is given by, $$\eqalign{
& {W_2} = \overrightarrow F .\overrightarrow s \cr
& {W_2} = 2 \times 39 \cr
& {W_2} = 78J \cr} $$

Work done by a variable force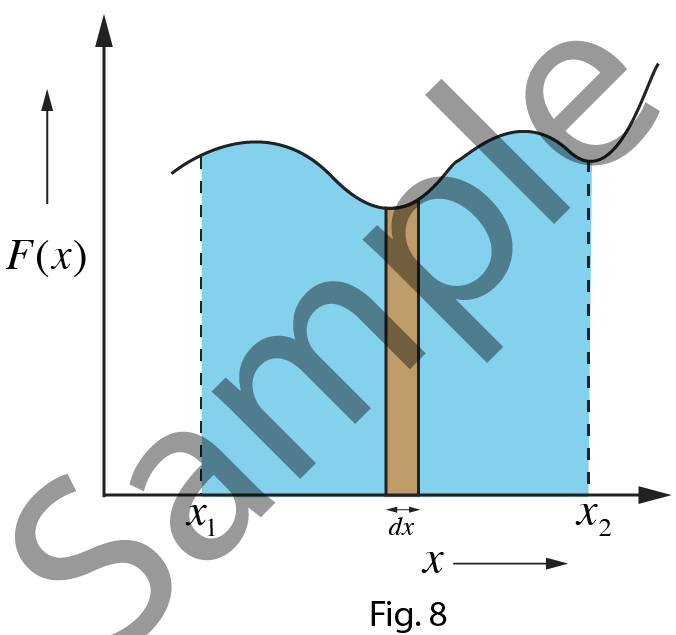

Let us consider a variable force $F$ acting on a body. The force $F$ is a function of $x$ as shown by the graphical relation.

Work done on a body by a variable force can be written as, $$ W = \int\limits_{{x_1}}^{{x_2}} {\overrightarrow F (x).d\overrightarrow x } $$

Area marked by brown color is the work done by a variable force in displacing a body by distance $dx$.

Area marked by sky blue color is the work done by a variable force in displacing the body from $x_1$ to $x_2$.

Question 5. A variable force $F=3x^2+2x$ is applied on a body. Find the work by the force in displacing the body along the $x$ axis by a distance $2m$ from the origin.

Solution: Work done is given as,$$\eqalign{
& W = \int {\overrightarrow F .d\overrightarrow x } \cr
& W = \int\limits_0^2 {\left( {3{x^2} + 2x} \right)dx} \cr
& W = \left[ {{x^3} + {x^2}} \right]_0^2 \cr
& W = 12J \cr} $$

Question 6. A force $\overrightarrow F = \left( {3{x^2}\widehat i + 2y\widehat j + 2\widehat k} \right)$ displaces a body from position $(2,3,4)$ to $(1,2,3)$. Find the work done.

Solution: Small displacement in 3D space is given as, $d\overrightarrow r = \left( {dx\widehat i + dy\widehat y + dz\widehat k} \right)$.

Therefore the work done is, $$\eqalign{
& W = \int\limits_{(2,3,4)}^{(1,2,3)} {\overrightarrow F .d\overrightarrow r }   \cr
& W = \int\limits_{(2,3,4)}^{(1,2,3)} {\left( {3{x^2}\widehat i + 2y\widehat j + 2\widehat k} \right).\left( {dx\widehat i + dy\widehat y + dz\widehat k} \right)}   \cr
& W = \int\limits_{(2,3,4)}^{(1,2,3)} {\left( {3{x^2}dx + 2ydy + 2dz} \right)}   \cr
& W = \left[ {{x^3}} \right]_2^1 + \left[ {{y^2}} \right]_3^2 + \left[ {2z} \right]_2^1 \cr
& W = (1 - 8) + (2 - 9) + (2 - 4) \cr
& W = - 16J \cr} $$

Spring Force

Consider a situation when one end of a spring is attached to a fixed wall and other end to a block, which is free to move on a horizontal table. The force due to spring is known as tension.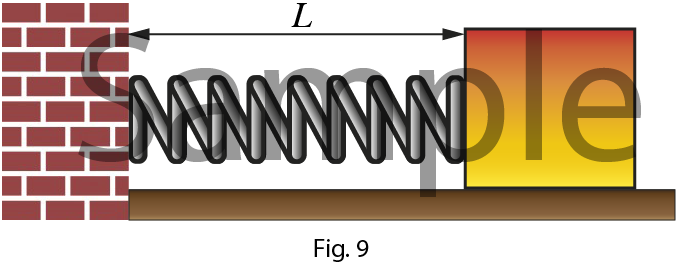 Tensional force is always opposite to the displacement. The natural length of the spring is $L$ and the spring constant is $k$.

According to Hooke’s law, the tension in a spring is proportional to the extension or compression. $$\eqalign{
& {F_T} \propto x \cr
& {F_T} = - kx \cr} $$

Negative sign states that the displacement and tensional force are in opposite direction.

Mechanism of spring

Spring in its natural length, therefore $x=0$ As, ${F_T}=-kx=0$ So, ${F_Ext}=0$
Here, the spring has enlongation $x$. Therefore, ${F_T}=-kx$ (-ve sign indicated that force is towards left and the displacement is towards right. So, force and displacement are in opposite direction. External force, ${F_Ext}=kx$	During elongation of the spring, the tension force is towards the spring
Here, the spring has enlongation $x$. Therefore, ${F_T}=-kx$ (-ve sign indicated that force is towards right and the displacement is towards left. So, force and displacement are in opposite direction. External force, ${F_Ext}=kx$	During compression of the spring, the tension force is away from the spring

Work done by a spring force

When the spring is elongated by a distance $x$ we get, $$\eqalign{
& {F_{Ext}} = kx ...(i) \cr
& {F_T} = - kx ...(ii) \cr} $$

Work done by the spring force is, $$\eqalign{
& {W_S} = \int\limits_0^x {{{\overrightarrow F }_T}.d\overrightarrow x }   \cr
& {W_S} = \int\limits_0^x {\left( { - kx} \right)dx}   \cr
& {W_S} = - \int\limits_0^x {kxdx}   \cr
& {W_S} = - \frac{k}{2}\left[ {{x^2}} \right]_0^2 \cr
& {W_S} = - \frac{1}{2}k{x^2}...(iii) \cr} $$

As we know that the potential energy stored in the spring will be negative of the work done by the conservative forces. Therefore, $$\Delta U = \frac{1}{2}k{x^2}...(iv)$$

Note: Whether the spring is elongated or compressed the potential energy stored in both the situation is $\Delta U = \frac{1}{2}k{x^2}$

Work done on a spring by an external force

When an external force ${\overrightarrow F _{Ext}}$ is applied on a spring and it undergoes an elongation of distance $x$,
From FBD, when the spring is elongated by a distance $x$ we get, $${\overrightarrow F _{Ext}} = kx$$
Work done by an external force to displace the spring by an infinitesimal distance $dx$ we get, $$\eqalign{
& {W_{Ext}} = \int\limits_0^x {{{\overrightarrow F }_{Ext}}.d\overrightarrow x } \cr
& {W_{Ext}} = \int\limits_0^x {kxdx} \cr
& {W_{Ext}} = \frac{1}{2}k\left[ {{x^2}} \right]_0^x \cr
& {W_{Ext}} = \frac{1}{2}k{x^2}...(v) \cr} $$
From equations $(iii)$ & $(v)$ we get, $$\eqalign{
& {W_S} = - \frac{1}{2}k{x^2} \cr
& {W_{Ext}} = \frac{1}{2}k{x^2} \cr} $$ or $${W_S} = - {W_{Ext}}$$

Question 7. Find the work done by a spring $(k=10N/m)$, when it elongates by a distance of $0.3m$. Also find the potential energy stored in the spring.

Solution:
Given,$$\eqalign{
& k = 10N/m \cr
& x = 0.3m \cr} $$
Work done by a spring is given by, $$\eqalign{
& {W_S} = - \frac{1}{2}k{x^2} \cr
& {W_S} = - \frac{1}{2}\left( {10} \right){\left( {0.3} \right)^2} \cr
& {W_S} = - 0.45J \cr} $$
Potential energy is the negative of the work done by spring, $$\Delta U = - {W_S} = 0.45J$$

Graph


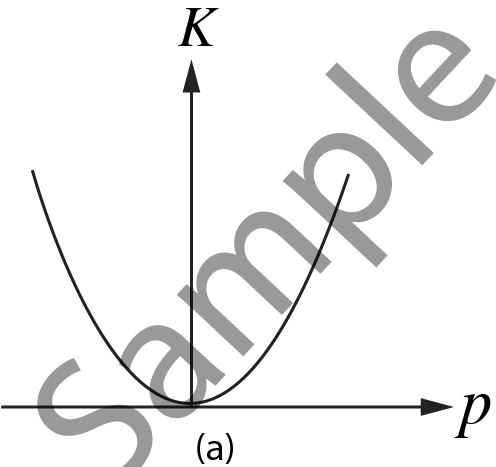
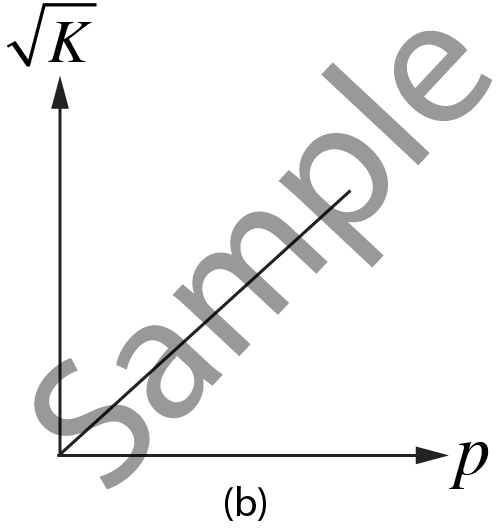
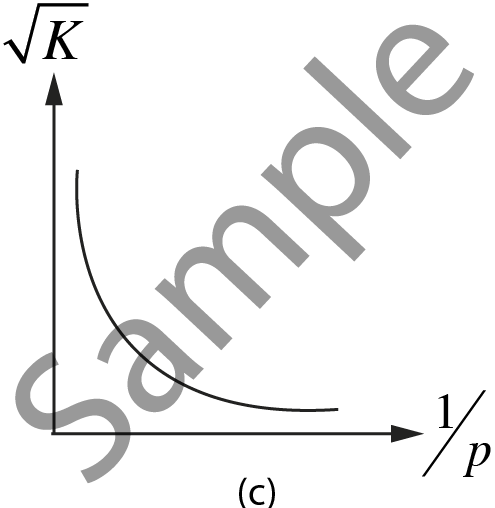
For $K = \frac{{{p^2}}}{{2m}}$, graph between $K$ and $p$ is a parabola.	For $p = \sqrt {2mK} $, graph between $\sqrt{K}$ and $p$ is a straight line.	For $\sqrt K \left( {\frac{1}{p}} \right) = \frac{1}{{\sqrt {2m} }}$, graph between $\sqrt{K}$ and $\frac{1}{p}$ is a hyperbola.

Let us analyze and compare the above situation in inertial and non-inertial frame of refernece.

Frame	Inertial frame of reference	Non-inertial frame of reference
FBD
Forces	$$f=ma$$	$$\eqalign{ & f = ma \cr & {F_p} = ma \cr} $$
Work done	Net work done on the block for displacement $s$, $${W_{net}}=mas$$	Net work done on the block for displacement $s$, $${W_{net}}=mas-mas$$
Work energy theorem	Work done by all the forces $(W_{net})$ = change in kinetic energy $\left( {\Delta K{E_{inertial}}} \right)$ in an inertial frame of reference. $$\eqalign{ & {W_{net}} = \Delta K{E_{inertial}} \cr & mas = \frac{1}{2}m{\left( {{v_b}} \right)^2} \cr & {v_b} = \sqrt {2as} \cr} $$	Work done by all the forces including pseudo force $(W_{net})$ = change in kinetic energy $\left( {\Delta K{E_{non-inertial}}} \right)$ in a non-inertial frame of reference. $$\eqalign{ & {W_{net}} = \Delta K{E_{non - inertial}} \cr & mas = \frac{1}{2}m{\left( {{v_{bt}}} \right)^2} \cr & {v_{bt}} = 0 \cr & \therefore {v_b} = {v_t} \cr} $$

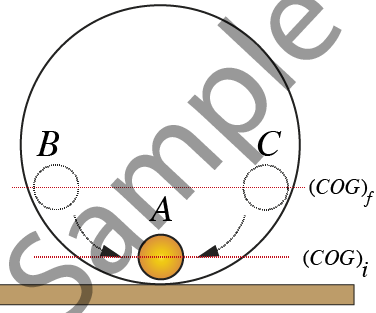
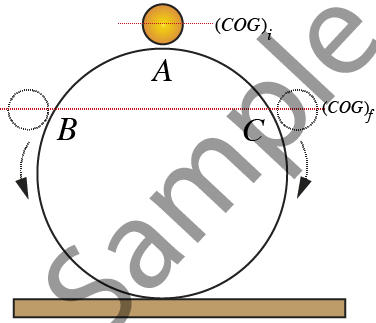
Type	Stable equilibrium	Unstable equilibrium	Neutral equilibrium
Illustration
Gradient	$\frac{dU}{dr}=0$, or gradient of $U-r$ graph is zero	$\frac{dU}{dr}=0$, or gradient of $U-r$ graph is zero	$\frac{dU}{dr}=0$, or gradient of $U-r$ graph is zero
Center of gravity $\left( {COG} \right)$	$\left( {COG} \right)$ of an equilibrium position is lower than that of the displaced position	$\left( {COG} \right)$ of an equilibrium position is higher than that of the displaced position	$\left( {COG} \right)$ of an equilibrium position and displaced position remains at the same level
Restoring force	When displaced from its equilibrium position a net restoring force starts acting on the body which has tendency to bring the body back to its equilibrium position.	When displaced from its equilibrium position, a net force starts acting on the body which moves the body away from the equilibrium position.	When displaced from its equilibrium position the body has neither the tendency to come back nor to move away from the original position.
Potential energy	Potential energy in this equilibrium position is minimum. $$\frac{{{d^2}U}}{{d{r^2}}} > 0$$	Potential energy in this equilibrium position is maximum. $$\frac{{{d^2}U}}{{d{r^2}}} < 0$$	Potential energy constant. $$\frac{{{d^2}U}}{{d{r^2}}} = 0$$
Examples	Pendulum oscillation	Ball rolling down an inclined wedge	Ball rolling on a horizontal surface
From Fig. 38	Point $B$ is stable equilibrium position	Point $C$ is unstable equilibrium position	Point $A$ is neutral equilibrium position